Phénomènes fondamentaux et postulats de l'électromagnétisme

Cette page fait site WikiSbec de Sébastien Bruneau.
Si vous êtes perdu, vous pouvez retourner à l'accueil en cliquant ici , ou au portail des sites sbeccompany.fr en cliquant ici

Accueil | Physique | Cours de physique | Phénomènes fondamentaux et postulats de l'électromagnétisme

Les premiers aimants connus étaient constitués d'un minerai naturellement magnétique découvert, dès l'antiquité, à proximité de la ville de Magnésia (Turquie) et appelé, pour cela, magnétite. Les propriétés de ces aimants naturels ont été mises à profit par les chinois qui ont confectionné, il y a déjà plus de mille ans, les premières boussoles. La preuve de l'existence d'un lien entre phénomènes électriques et magnétiques est beaucoup plus récente puisqu'elle ne date que du 18ème siècle. En effet, si l'on avait depuis longtemps remarqué que certaines parties métalliques des navires s'aimantaient, par exemple, lorsque ceux-ci étaient frappés par la foudre, il fallut attendre les travaux de Benjamin Franklin sur la foudre pour que naisse l'idée d'une possible communauté de nature entre électricité et magnétisme. Une formulation reliant ces deux phénomènes entre eux, n'a cependant été élaborée qu'au 19ème siècle par Maxwell qui a proposé, vers 1873, un jeu d'équations dont l'interprétation complète n'a pu être donnée qu'en 1905, dans le cadre de la théorie de la relativité développée par Einstein.

Nous présentons, ci-dessous, les expériences fondamentales qui mettent en évidence les effets magnétiques de l'électricité, ainsi que les postulats qui en découlent et fondent ce qu'il est convenu d'appeler l'électromagnétisme (sous une forme plus complète et plus élaborée, ces postulats se condensent en un jeu d'équations appelées équations de Maxwell).

Forces s'exerçant entre circuits électriques

L'expérience montre que deux fils conducteurs parcourus par des courants électriques s'attirent si les courant sont de même sens et se repoussent s'ils sont de sens opposé.

La loi de Coulomb étudiée au chapitre précédent ne pennet pas d'expliquer ces actions. En effet, si on admet généralement que, sur les conducteurs, existent des charges superficielles immobiles qui créent un champ électrostatique auquel sont soumises les charges participant au courant, leur densité surfacique est bien trop faible pour rendre compte des forces qui se manifestent, dans ce cas, entre les fils. Quant aux autres charges intérieures à chacun des deux conducteurs (ions fixes du réseau et électrons libres), elles se compensent mutuellement et ne peuvent donc créer de forces d'un fil à l'autre.

On constate les mêmes phénomènes d'attraction et de répulsion entre circuits de formes quelconques. Ces phénomènes sont donc généraux et conduisent à postuler que deux charges en mouvement l'une par rapport à l'autre exercent entre elles une force, qualifiée de force électromagnétique.

Conception ampérienne du magnétisme

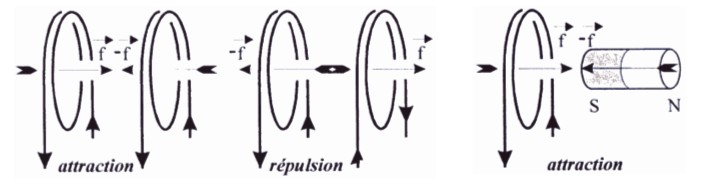
Deux fils conducteurs enroulés sous forme de bobines (solénoïdes) et mis en vis à vis comme le montre la figure 3.1.2.a, exercent l'un sur l'autre des forces (électromagnétiques) lorsqu'ils sont parcourus par des courants. Le sens de ces forces dépend des sens respectifs de rotation des courants dans les deux spires: si ces sens sont les mêmes, les bobines s'attirent; s'ils sont opposés, elles se repoussent.

Lorsqu'on remplace l'un des deux solénoïdes par un barreau aimanté (voir figure), il y a répulsion ou attraction selon l'orientation du barreau et le sens du courant dans le solénoïde restant. C'est ce phénomène qui a conduit Ampère à conjecturer l'existence, dans la matière aimantée, d'un très grand nombre de courants circulaires orientés de la même façon et produisant les mêmes effets magnétiques qu'une bobine.

On explique, aujourd'hui, l'origine du magnétisme par le « mouvement» des électrons liés aux atomes (mouvement orbital autour du noyau, et mouvement de rotation sur eux-mêmes). Nous nous contenterons, dans ce module, de reprendre l'hypothèse d'Ampère en admettant l'existence de courants circulaires microscopiques généralement appelés courants ampériens (ou « ampériens » tout court).

Force électrique, force magnétique, force de Lorentz

Considérons, dans le vide, un système de charges en mouvement dans un repère [R] attaché un référentiel galiléen (par exemple un courant électrique d'intensité constante ou variable, dans un circuit quelconque). L'expérience montre qu'une charge ponctuelle q se trouvant, à l'instant t, en un point M au voisinage de ce système, subit une force <math>\vec{f}</math> proportionnelle à q. Deux cas peuvent alors se présenter :

q possède une vitesse nulle dans [R], alors <math>\vec{f}</math> se réduit à une force électrique <math>\vec{f_e}</math> que l'on pose telle que :

la grandeur vectorielle <math>\vec{E}</math> étant appelée champ électrique (non assimilable, sauf conditions particulières, au champ électrostatique <math>\vec{E_s}</math> ;

q possède en M une vitesse <math>\vec{v}</math> non nulle dans [R] ; alors, à la force précédente s'ajoute une autre force <math>\vec{f_m}</math> orthogonale à <math>\vec{v}</math> et proportionnelle à son module <math>\left| \vec{v} \right|</math>, dite force magnétique (parfois nommée force de Laplace ou de Lorentz) ; cette force est posée telle que :

<math>\vec{f_m}=q \vec{v} \wedge \vec{B}</math>

relation dans laquelle la grandeur vectorielle <math>\vec{B}</math> désigne un nouveau champ appelé champ magnétique. Au bilan on a donc :

<math>\vec{f} = q \left( \vec{E} + \vec{v} \wedge \vec{B} \right)</math>

expression connue sour le nom de force de Lorentz, qui définit à la fois le champ électrique <math>\vec{E}</math> et le champ magnétique <math>\vec{B}</math> produit au point M par le systèm de charges en mouvement, et constitue un postulat fondamental de la physique. Cet ensemble de deux champs est ce que l'on appelle le champ électromagnétique.

Le champ électrique a les mêmes dimensions que le champ électrostatique, et s'exprime pour cela en V.m^-1.

D'après la définition de la force magnétique, le champ magnétique a pour dimensions :

Son unité dans le SI est le Tesla de symbole T. On utilise aussi le Gauss de symbole G, égal à 10^-4 T.

Remarques

Si toutes les charges du système sensé produire le champ électromagnétique (<math>\vec{E}</math>,<math>\vec{B}</math>) sont immobiles dans [R], ce champ se réduit évidemment au seul champ électrostatique <math>\vec{E_s}</math>.
S'il existe deux systèmes de charges distincts créant chacun en M un champ électrique et un champ magnétique particulier, les champs électrique et magnétique résultants en M, sont les sommes vectorielles respectives de ces champs électriques et magnétiques particuliers. Cette proposition est connue sous le nom de théorème de superposition.
Un changement de référentiel galiléen modifie <math>\vec{E}</math>, <math>\vec{B}</math> et <math>\vec{v}</math>, donc les forces électriques et magnétique. Mais, tant que <math>\vec{v}</math> reste petite devant la vitesse de lumière, ces modifications se comensent de sorte que la force de Lorentz peut être considérée comme invariante.

Applications

Trajectoire d'une charge ponctuelle dans un champ magnétique uniforme

Considérons, dans un repère [Oxyz] attaché à un référentiel galiléen, une charge ponctuelle q de masse m, animée d'une vitesse <math>\vec{v}</math>. Supposons, de plus, que dans l'espace ainsi défini, règne un champ magnétique uniforme tel que <math>\vec{B}=B \vec{k}</math>. Cette charge subit donc la force magnétique <math>\vec{f}_m</math> et, d'après le PFD, on a :

<math>m \frac{d\vec{v}}{dt}=q\vec{v} \wedge \vec{B}</math>

soit :

<math>\frac{dv_x}{dt}\vec{i}+\frac{dv_y}{dt}\vec{j}+\frac{dv_z}{dt}\vec{k}=\frac{qB}{m} \left(v_x \vec{i} \wedge \vec{k} + v_y \vec{j} \wedge \vec{k} + v_z \vec{k} \wedge \vec{k} \right) =\frac{qB}{m} \left( -v_x \vec{j} + v_y \vec{i} \right) </math>

par conséquent :

<math>\left{ { \frac{dv_x}{dt} = + \frac{qB}{m}v_y \text{ }(a) \\ \frac{dv_y}{dt} = + \frac{qB}{m}v_x \text{ }(b) \\ \frac{dv_z}{dt} = 0 \text{ }\Rightarrow\text{ } v_z=const. } \right.</math>

soit, en dérivant (a) et (b) par rapport à t :

<math>\left{ { \frac{d^2v_x}{dt^2} = + \frac{qB}{m}\frac{dv_y}{dt}=- \left( \frac{qB}{m} \right)^2 v_x \text{ } \Rightarrow \text{ } v_x=C \cos{( \omega }t + \varphi )} \\ { \frac{d^2v_y}{dt^2} = - \frac{qB}{m}\frac{dv_x}{dt}=- \left( \frac{qB}{m} \right)^2 v_y \text{ } \Rightarrow \text{ } v_y=D \cos{( \omega }t + \psi )} \right.</math>

avec <math>\omega = \frac{qB}{m} </math>

En choisissant alors <math>\varphi = 0</math> et <math>\vec{v} = v_0 \vec{i}</math> à t = 0, on obtient <math>C = v_0</math> et <math>\psi = \pi / 2 \Rightarrow v_x=v_0 \cos {(\omega t)}</math> et <math>v_y = -D \sin {(\omega t)}</math>. Alors, comme <math>dv_y/dt=-(qB/m)v_x=-\omega v_x</math>, on peut écrire <math>-D \omega \cos {(\omega t)} = -\omega v_0 \cos {(\omega t)}</math> ; d'où il vient que <math>D = v_0</math>, soit :

<math>\left{ {v_x = v_0 \cos {(\omega t)}} \\ {v_y = -v_0 \sin {(\omega t)}} \right.</math>

En intégrant une dernière fois et en choisissant (arbitrairement) x=0 et <math>y=v_0/\omega</math> à t=0, on obtient ainsi :

<math>\left{ {x=\frac{v_0}{\omega}\sin{(\omega t)}+const.= \frac{mv_0}{qB} \sin {(\omega t )}+0 } \\ {y=\frac{v_0}{\omega}\cos{(\omega t)}+const.= \frac{mv_0}{qB} \cos {(\omega t )}+0 } \right.</math>

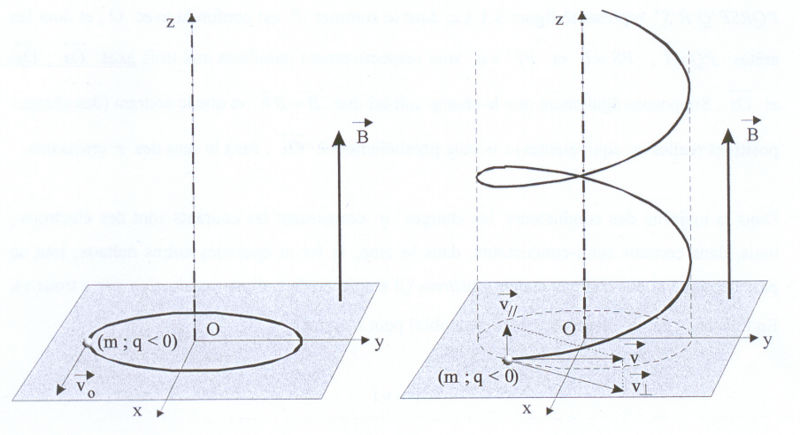
qui sont les équations paramétriques d'une trajectoire circulaire de centre O, de rayon <math>v_0/ \left| \omega \right| = mv_0 / \left|q \right| B</math>, parcourue avec une vitesse de module constant v₀ (schéma suivant).

Remarques

On vérifie qu'un électron (charge q=-e), décrit sa trajectoire dans le sens direct.
Une particule chargée pénétrant transversalement un champ magnétique se met ainsi à décrire un cercle; elle y est donc non seulement déviée, mais elle s'y trouve piégée.
Dans le cas général, la vitesse initiale d'une particule chargée dans un champ magnétique peut s'écrire comme la somme d'une composante orthogonale au champ, et d'une composante qui lui est parallèle, soit <math>\vec{v}=\vec{v}_{\perp}+\vec{v}_{//}</math>. Il s'ensuit que la particule décrit dans ce champ une hélice (voir deuxième schéma ci dessus d'axe parallèle au champ et de rayon <math>R = m \left| \vec{v}_{\perp} \right| / q \left| \vec{B} \right| </math> et progresse selon une direction du champ à la vitesse constant <math> \vec{v}_{//} </math> puisque aucune force n'est appliquée dans cette direction.

Effet Hall

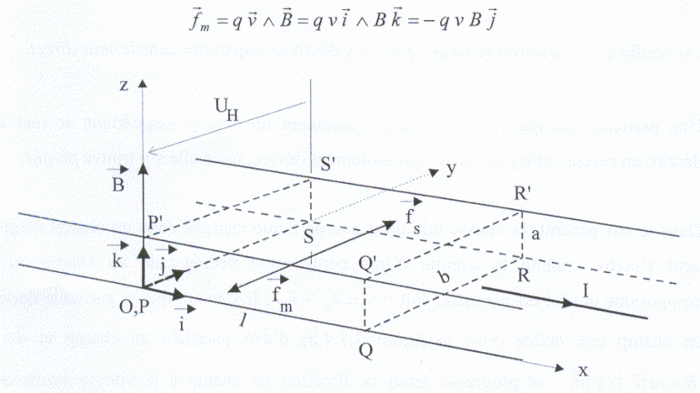
Considérons, dans un repère [Oxyz] attaché à un référentiel galiléen, une portion d'un conducteur fixe parcouru par un courant constant d'intensité I et plongé dans un champ magnétique uniforme B. Supposons que cette portion ait la forme du parallélépipède rectangle PQRSP'Q'R'S' représenté dans la figure suivante, dont le sommet P est confondu avec O, et dont les arrêtes PQ = l, PS = b, PP' = a sont respectivement parallèles aux trois axes Ox, Oy et Oz. Supposons également que le champ soit tel que B soit sur l'axe des z, et que le courant s'écoule parallèlement à Ox, dans le sens des x croissants.

Dans la majorité des conducteurs, les charges q constituant les courants sont des électrons; mais, dans certains semi-conducteurs, dans le zinc, le fer et quelques autres métaux, tout se passe comme si ces charges étaient positives (il s'agit, en fait, d'une conduction par « trous »). En l'absence de B , leur vitesse (d'ensemble) est selon l'axe des x, positif. On a v>0 si q>0 et v<0 si q<0, étant donné le sens choisi pour le courant. En présence de B, chaque charge est donc soumise à la force magnétique, donnée sur la figure ci dessous :

Comme v et q sont du même signe, le produit qv est toujours positif et le sens de fm est toujours opposé à celui de j, vecteur unitaire des Oy. Il se produit donc, du côté PQQ'P' du ruban, une accumulation des charges en mouvement, lecôté SRR'S' s'en trouvant dégarni par compensation et prenant, de ce fait, une charge de signe contraire. La polarisation opposée de ces deux côtés crée dans le ruban, un champ électrostatique (supposé uniforme) E_H sur l'axe des y, dit champ de Hall, tel que E_H > 0 si q > 0 et. E_H < 0 si q < 0 .

Le Le champ de Hall exerce, à son tour, la force électrostatique <math>\vec{f}_s=q \vec{E}_H = qE_H \vec{j}</math> sur les charges en mouvement, force qui est de même sens que j puisque le produit qE_H est toujours positif. En régime permanent f_s équilibre alors f_m, et l'on peut écrire :

<math>\vec{f}_s=-\vec{f}_m \Rightarrow q\vec{E}_H = qvB \vec{j} \Rightarrow \vec{E}_H=vB\vec{j} </math>

Il s'établit ainsi entre PQQ'P' et SRR'S' une différence de potentiel telle que :

<math>U_H=V_P-V_S=\int\limits_S^PdvV=\int\limits_S^P-\vec{E}_Hdy\vec{j}=-\int\limits_{y=b}^{y=0}vBdy=vBb</math>

dite tension de Hall, dont on voit qu'elle est du même signe que v, donc que q. Pour faire apparaître l'intensité I dans la tension de Hall, il suffit de se rappeler que si le vecteur densité de courant J = n q v = n q v i (que l'on ne confondra pas, ici, avec le vecteur unitaire de l'axe oy des coordonnées cartésiennes !) est unifonne, et si S est une section droite du conducteur munie du vecteur unitaire normal N = i , on a :

<math>I=\int\int\limits_S\vec{j}\vec{N}d^2S=nqv\int\limits_S d^2S=nqvab \Rightarrow vb=\frac{I}{nqa}</math>

n étant la densité volumique des charges. Il s'ensuit que :

RH = 1/nq étant appelé constante de Hall.

Remarque

L'effet Hall a des applications importantes puisque le sens et la valeur de la tension de Hall permettent de déterminer, pour un conducteur solide, le signe des charges en mouvement et leur densité volumique. En outre, l'intensité I étant connue, la mesure de U_H permet de déterminer B ( « sonde de Hall »). Par exemple, avec B = 1 T , 1 = 10 A et a = 0,1 mm , on obtient U_H = -5,5 μV pour le cuivre; on en déduit que les charges en mouvement sont des électrons (puisque U_H < 0), que la constante de Hall vaut R_H = -5,5.10^-11 C^-1 m³ et que la concentration en électrons libres est n =1/ R^H q =1,1.10²⁹ m^-3.

Flux du champ magnétique

Propriété de conservation du flux

Considérons, dans une zone où existe un champ magnétique B, une surface fermée Σ quelconque munie, en chacun de ses éléments d²Σ, d'un vecteur unitaire normal sortant N. Alors, par propriété, le flux de B sortant de Σ, est nul; ce qui s'écrit:

<math>\Phi=\oint\int\limits_\Sigma\vec{B}\vec{N}d^2\Sigma=0</math>

et s'énonce comme :

LE FLUX DU CHAMP MAGNETIQUE SORTANT D'UNE SURFACE FERMEE QUELCONQUE EST NUL

Cette loi est générale et reste valable, même en régime variable. Elle implique que :

le flux du champ magnétique à travers une surface ouverte s'appuyant sur un contour fermé, ne dépend pas du choix de cette surface.

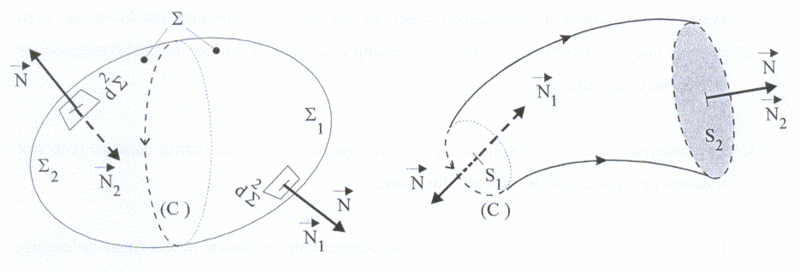
Soit, en effet, les deux surfaces ouvertes Σ1 et Σ2 s'appuyant sur le même contour fermé (C) (voir figure suivante) ; pour déternliner les flux Φ1 et Φ2 qui les traversent respectivement, il faut convenir du sens de leurs vecteurs unitaires nomlaux respectifs en tout point, N1 et N2 .Pour cela, il est commode de se fixer (arbitrairement) un sens de parcours de (C), et de choisir pour sens des unitaires nOrnlaux celui dans lequel progresserait un tire-bouchon tournant dans ce sens de parcours. On peut considérer, maintenant, que l'ensemble des deux surfaces forme une surface fermée Σ au travers de laquelle le flux sortant est nul par propriété. Or, si le vecteur unitaire N sortant de Σ par Σ1 , est de même sens que N1 , on montre que celui sortant de Σ par Σ2 est nécessairement de sens opposé à N2 (et vice-versa). Ainsi, si le flux sortant de Σ par Σ1 est Φ1, et celui sortant de Σ par Σ2 est -Φ2, on a Φ1 + (-Φ2) = 0 d'où Φ1 = Φ2.

Lignes de champ et tubes de champ

Comme le champ électrique, le champ magnétique suit des lignes de champ (courbes en tout point desquelles il est tangent). On appelle tube de champ un ensemble de lignes de champ s'appuyant sur un contour fenmé. Il est facile de voir que: à l'intérieur d'un tube de champ, le flux se conserve (c'est-à-dire, est le même à travers n'importe quelle section considérée du tube). Soit, en effet, une surface Σ constituée d'un tube de champ fermé par deux section quelconques S1 et S2, et soit (C) le contour orienté de S1. Le flux sortant de Σ étant nul par propriété, et celui sortant par les parois du tube étant encore nul du fait que le champ y est tangent en tout point par nature, le flux sortant de Σ par S1 est l'opposé de celui sortant de Σ par S2. Mais si le flux sortant par S1 a même signe que celui traversant cette surface (selon la convention de signe imposée par l'orientation du contour (C)), celui sortant par S2 sera de signe opposé au flux qui traverse cette autre surface (selon la même convention de signe). Il s'ensuit que les flux traversant S1 et S2 ont la même valeur absolue et même signe.

Remarques

L'unité de flux de champ magnétique dans le Si est le Weber (Wb).
Du fait de la conservation du flux du champ magnétique, un tube de champ créé par des systèmes de courants de dimensions finies, se referme nécessairement sur lui-même. Il en découle que, contrairement aux lignes de champ électrique, les lignes de champ magnétique se referment sur elles-mêmes.
La conservation du flux implique, également, que le module du champ dans un tube soit d'autant plus grand que le tube est plus étroit.
Les effets les plus spectaculaires et les plus connus dans la nature, de ces tubes de champ, sont les taches que l'on observe à la surface du soleil.

Portail de la physique – Accédez aux articles du Wikisbec concernant la physique.